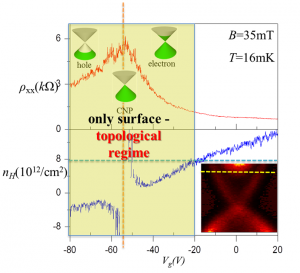
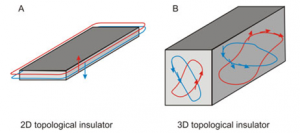
 We study quantum-transport phenomena and electron-dynamics associated with topological phases of matter. New phases in certain chalcogenides that are characterized by nontrivial topological orders associated with the bands are interesting because they have new characteristic properties that differ from symmetry breaking states. The characteristic properties of topological orders include fractional statistics (such as non-Abelian statistics), fractional charges, and topologically protected gapless boundary-excitations. For example, a topological insulator has gapless boundary-states with an insulating bulk, and the boundary states can produce Majorana fermions when coupled to an s-wave superconductor. Majorana fermions are expected to follow non-Abelian statistics, which can be used to perform fault-tolerant topological quantum computations.
We study quantum-transport phenomena and electron-dynamics associated with topological phases of matter. New phases in certain chalcogenides that are characterized by nontrivial topological orders associated with the bands are interesting because they have new characteristic properties that differ from symmetry breaking states. The characteristic properties of topological orders include fractional statistics (such as non-Abelian statistics), fractional charges, and topologically protected gapless boundary-excitations. For example, a topological insulator has gapless boundary-states with an insulating bulk, and the boundary states can produce Majorana fermions when coupled to an s-wave superconductor. Majorana fermions are expected to follow non-Abelian statistics, which can be used to perform fault-tolerant topological quantum computations.
